"얼마나 효율적인가?" (시간/메모리/리소스)
1. 수행 시간 측정 (직접 구현 O )
→ 동일한 하드웨어를 사용하여 실제 수행 시간을 측정한다.
2. 알고리즘의 복잡도 측정 (직접 구현 X)
→ 연산의 횟수를 계산하여 비교한다. (예측)
→ 연산의 횟수는 n의 함수 (n은 충분히 큰 양의 정수. 즉, 입력의 크기에 따른 연산 횟수를 계산한다.)
수행 시간 측정 2가지 방법
#include <time.h>
start = clock(); // 시작 전 check
// 알고리즘 내용 삽입 부분
stop = clock(); // 종료 직후 check
double duration = (double)(stop - start) / CLOCK_PER_SEC;<일반으로 사용하는 방법 #1>
#include <time.h>
start = time(NULL);
//알고리즘 내용 삽입 부분
stop = time(NULL);
double duration = (double)difftime(stop,start);<방법 #2>
알고리즘의 복잡도(Complexity) 분석 방법
공간 복잡도 (Space Complexity)
▶ 메모리 사용량에 대한 분석 결과.
시간 복잡도 (Time Complextiy)
▶ 알고리즘을 이루고 있는 연산들이 주어진 입력 n에 대해 몇 번이나 수행되는지를 숫자로 표시.
▶ 속도에 해당하는 알고리즘의 수행 시간 분석 결과.
▶ 보통 알고리즘의 복잡도를 논할 때는 시간 복잡도를 말한다.
#수도코드 #연산횟수
largest <- scores[0] //대입 연산 1회
for i <- to N-1 do // (n-1)반복 4~6번 코드 => 2*(n-1)
if scores[i]>largest //비교 연산 1회
then largest <- scores[i] //대입 연산 1회
return largest // 반환 연산 1회
// 1+2n-2+1 = 2n (총 연산 횟수) (n : 입력의 크기)
<복잡도 분석 예시>
| 알고리즘 A | 알고리즘 B | 알고리즘 C |
| sum <- n*n; | for i <- 1 to n do sum <- sum + n; |
for i <- 1 to n do for j<- to n do sum <- sum+1; |
| 곱셈 연산 1회, 대입 연산 1회 | (덧셈 연산 1회, 대입 연산 1회) -> n번 반복 // 덧셈 연산 n회, 대입 연산 n회 |
(덧셈 연산 1회, 대입연산 1회) -> n^2번 반복 // 덧셈 연산 n*n회, 대입 연산 n*n회 |
| 2 | 2n | 2n^2 |
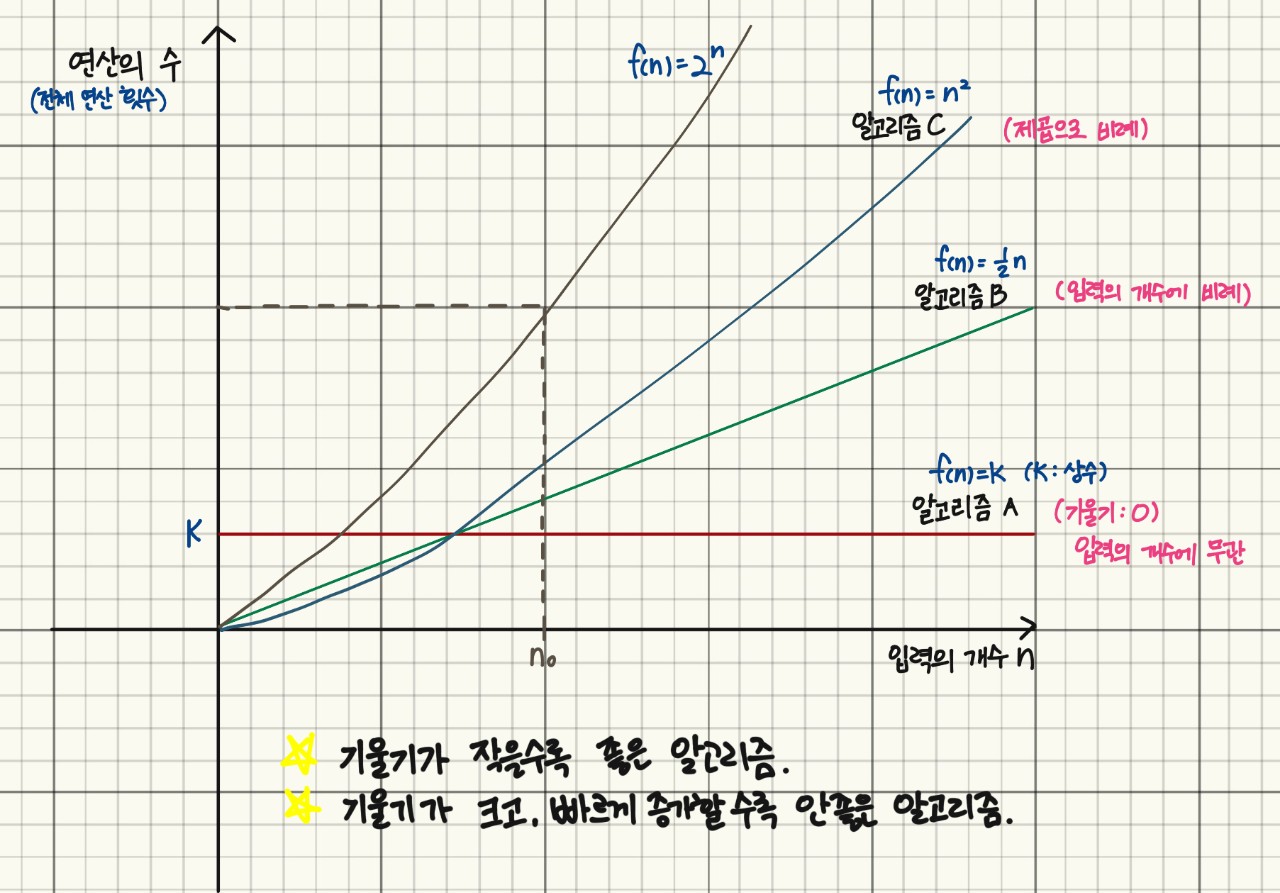
빅오 표기법 (Big-O Notation)
▶ 입력 자료의 개수가 충분히 큰 경우에는, 차수가 가장 큰 항이 가장 영향을 크게 미치고 다른 항들을 상대적으로 무시될 수 있음.
▶ T(n) = n^2 + n + 1을 예로 들어보자.
n = 1000인 경우 (n이 매우 클 때), T(n)을 전개하면
T(n) = 10^6 + 10^3 + 1 = 1,001,001이다.
이때, n^2이 99%, n+1이 0.1%를 차지하는 것을 볼 수 있다.
따라서, 차수가 가장 큰 항만 고려해도 시간 복잡도를 구할 수 있다.
▶ 연산의 횟수를 대략적(점근적)으로 표기한 것. (단, n은 충분히 크다고 가정)
▶빅오는 함수의 상한(Upper bound)을 표시한다.
※ 수학적 정의 : 두 개의 함수 f(n)과 g(n)이 주어졌을 때, 모든 n ≥ n0에 대하여(= n이 충분히 클 때) |f(n)| ≤ C|g(n)|을 만족하는 2개의 상수 C와 n0가 존재하면 f(n) = O(g(n))이다.
≫ 자료를 찾아보면, 빅오 표기법의 수학적 정의가 "모든 n>n0에 대하여"라고 나오는 곳도 있다. 빅오 표기법은 점근적 표기법으로, n은 '충분히 큰 수'를 의미하기 때문에 n0의 포함여부는 중요하지 않다. 하지만 정의에 따르면 상수 c와 n0가 존재해야 하므로 "모든 n ≥ n0에 대하여"라고 하는 것이 맞는 표현이다.

빅오 표기법의 종류 (크기 순서)
O(1) 상수형 < O(log n) 로그형 < O(√n) < O(n) 선형 < O(n log n) 선형 로그형 < O(n^2) 2 차형 < O(n^3) 3 차형 < O(2^n) 지수형 < O(n!) 팩토리얼형
쉽게 풀어쓴 C언어 예제 풀이

참고 서적 : <C언어로 쉽게 풀어쓴 자료구조>, <윤성우의 열혈 자료구조>
'Programming > 자료구조' 카테고리의 다른 글
| [자료구조] 06. 재귀 (Recursion) (0) | 2021.10.23 |
|---|---|
| [자료구조] 05. 알고리즘의 효율성 (최선, 평균,최악) (0) | 2021.10.22 |
| [자료구조] 04. 빅오메가 표기법 & 빅세타 표기법 (0) | 2021.10.21 |
| [자료구조] 02. 추상 데이터 타입 (0) | 2021.10.20 |
| [자료구조] 01. 자료 구조와 알고리즘 (0) | 2021.10.12 |



